In dieser kleinen GeoGebra-Werkstatt lernen wir anhand weniger typischer Probleme grundlegende Arbeitsweisen in GeoGebra. Für allgemeine Anleitungen zu GeoGebra (Installation, Bedienelemente usw.) und reichhaltige Materialsammlungen besuche man die Seiten von GeoGebra.org.
1. Analysis
Aufgabenstellung
Ermittle, für welchen Wert von a die Funktion ![]() an der Stelle 5 eine Normale mit der Steigung ‑5 hat. Bilde außerdem die Ableitungsfunktion von f.
an der Stelle 5 eine Normale mit der Steigung ‑5 hat. Bilde außerdem die Ableitungsfunktion von f.
Herangehensweise
- Die richtige Ansicht wählen:
Über das Menü Ansicht sollte man die Grafik-Ansicht (nicht Grafik 2) und die Algebra-Ansicht aktivieren. Mit einem Rechtsklick im Grafik-Bereich erscheint ein Menü, mit dessen Hilfe man Koordinatengitter und ‑achsen ein- oder ausblenden kann. - Den Funktionsparameter mit einem Schieberegler veränderbar gestalten:
Zunächst fügt man einen Schieberegler ein (zweite Schaltfläche von rechts mit der Kennzeichnung a=2). Man kann diverse Eigenschaften festlegen, mit denen man auch ein wenig herumexperimentieren sollte. - Die Funktionenschar eingeben:
In die Eingabeleiste unten (ggf. im Menü Ansicht einblenden) gibt man folgende Zeichenfolge ein: f_a(x)=(x – 2)/(10 (a – x)). Wichtig sind hier die Klammern, sonst versteht GeoGebra nicht, was im Bruch im Zähler bzw. Nenner stehen soll. Wie man sieht, kann man den Index mit einem geschützten Leerzeichen _ abtrennen. Sollen mehrere Zeichen in den Index, verwendet man {geschweifte Klammern}. - Einen Punkt auf f mit x=5 festlegen:
Man kann natürlich mithilfe der zweiten Schaltfläche von links ganz einfach einen Punkt auf dem Funktionsgraphen entstehen lassen. Leider wird man es je nach Funktion schwer haben, den Punkt exakt bei x=5 zu platzieren. Präziser ist es, wenn man folgendes in die Eingabezeile schreibt: P=(5,f_a(5)). - Zuerst eine Tangente konstruieren:
GeoGebra kann nicht direkt eine Normale an einem Funktionsgraphen bauen, daher müssen wir den Umweg über eine Tangente gehen. Man gibt entweder die Zeichenfolge Tangente[P, f_a] in die Eingabezeile ein oder benutzt die vierte Schaltfläche von links (Tangente im Schaltflächen-Menü auswählen). Die Tangente, die im Moment noch irgendeinen Buchstaben als Namen hat, benennen wir im Algebra-Fenster einfach in Tangente um. - Nun die Normale konstruieren:
Man kann auch hier entweder wieder die Eingabezeile oder eine Schaltfläche (vierte von links) benutzen. Die Eingabe lautet Senkrechte[P,Tangente]. - Ansichten anpassen:
Man kann nun die Tangente unsichtbar machen, indem man auf den blauen Kreis vor der Tangentengleichung im Algebra-Fenster klickt. Alternativ: Rechtsklick auf die Tangente im Grafik-Fenster, Objekt anzeigen abwählen.
Außerdem möchte man vielleicht die Normale in der Form y=mx+b anzeigen lassen. Dies gelingt nach einem Rechtsklick auf die Gleichung im Algebra-Fenster und der entsprechenden Menü-Auswahl. - Gesuchten Wert finden:
Nun manipuliert man solange am Schieberegler herum, bis man den gesuchten Wert findet. 🙂 - Ableitung bilden:
Das ist nun äußerst einfach. Man schreibt schnell in die Eingabezeile Ableitung[f_a]. Das war’s.
So sollte es am Ende aussehen:
2. Analytische Geometrie I
Aufgabenstellung
Die Ebene E verlaufe durch die drei Punkte A (0| 0| 1), B (4| 0| 1), C (4| 5| 0). Die Ebene F habe die Gleichung 4x‑z=-2. Bestimme eine Gleichung der Schnittgeraden sowie den Winkel zwischen E und F.
Herangehensweise
- Ansicht einstellen:
Für diese Aufgabe benötigen wir die 3D-Ansicht. Man wähle also diese im Ansichts-Menü und wähle ggf. die normale Grafik-Ansicht etc. ab. Die Algebra-Ansicht sollte jedoch erhalten bleiben. - Ebene E eingeben:
Die Ebene E kann man einfach in der Eingabezeile eingeben. Die Eingabezeile kann man, falls sie nicht zu sehen ist, über das Ansichts-Menü aktivieren. Man beginnt das Wort Ebene zu tippen, dann wird schon die Möglichkeit angeboten, drei Punkte einzugeben. Die komplette Zeile lautet dann: Ebene[(0, 0, 1), (4, 0, 1), (4, 5, 0)]. Die Ebene wird sofort in der 3D-Ansicht angezeigt. Die Ansicht kann man mit gedrückter rechter Maustaste leicht drehen. Wer schnell verwirrt ist, welche Achse welche ist, kann an eine leere Stelle in der 3D-Ansicht klicken, im Menü unten den Punkt Grafik… aufrufen und im erscheinenden Fenster bei den Achsen die Beschriftung aktivieren. - Ebene F eingeben:
Liegt eine Ebene in Koordinatenform vor, ist die Eingabe sehr einfach. Man muss lediglich die Gleichung in die Eingabezeile schreiben. Um sicherzustellen, dass die Ebene den Namen F trägt, gibt man vor der Gleichung F: ein. Nun sollte auch diese Ebene sichtbar sein. - Schnittgerade bestimmen lassen:
Die Eingabe Schneide[E,F] erzeugt die Schnittgerade. Wie man möglicherweise sieht, ist die Darstellung im Algebra-Fenster nicht optimal. Für eine Weiterbenutzung der Gerade sollte man ggf. den Richtungsvektor mit einer geeigneten Zahl multiplizieren, damit der Vektor angenehmer wird.
Einen schöneren Stützvektor kann man bekommen, indem man einen Punkt auf der Schnittgeraden platziert (zweite Schaltfläche von links) und diesen auf der Gerade etwas hin und her schiebt, bis man einen schöneren Punkt erhält. Leider erwischt man damit nicht unbedingt exakt die „schönen” Punkte, sondern Punkte, deren Koordinaten viele unbequeme Kommastellen haben. Daher muss man unter Umständen ein wenig selbst rechnen. - Schnittwinkel bestimmen lassen:
Das ist nun wieder sehr einfach. Man muss nur in die Eingabezeile tippen: Winkel[F, E].
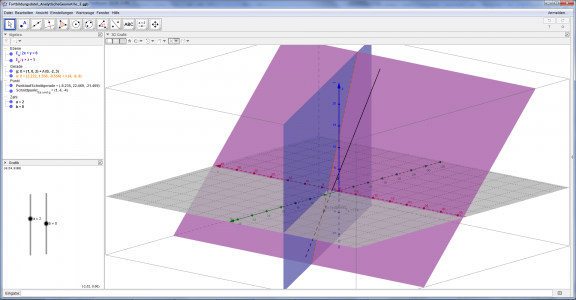
So sollte es am Ende aussehen:
3. Analytische Geometrie II
Aufgabenstellung
Überprüfe, welche Lagebeziehung die Ebenen der Schar ![]() zueinander haben und bestimme den Schnittpunkt der Geraden
zueinander haben und bestimme den Schnittpunkt der Geraden 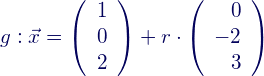 mit
mit ![]() .
.
Herangehensweise
- Ansicht einstellen:
Für diese Aufgabe benötigen wir die 3D-Ansicht. Man wähle also diese im Ansichts-Menü und wähle ggf. die normale Grafik-Ansicht etc. ab. Die Algebra-Ansicht sollte jedoch erhalten bleiben.
Für die Ebenenschar benötigen wir aber auch einen Schieberegler. Diesen kann man nicht in der 3D-Ansicht unterbringen. Daher brauchen wir eine normale Grafik-Ansicht. Diese kann man aber platzsparend unter die Algebra-Ansicht schieben. - Schieberegler erstellen:
Den Schieberegler erstellen wir wie bereits angedeutet, im Grafik-Fenster. Wenn man möchte, dass nur ganze Zahlen benutzt werden, kann man das in den Schieberegler-Einstellungen auswählen. - Ebenenschar aufstellen:
Nun geht man wieder in das 3D-Fenster und schreibt in die Eingabezeile (ggf. im Menü Ansicht einblenden) E_a: 2a x + 2y + (2 – a) z = 5a + 2. Jetzt kann man mithilfe des Schiebereglers die Ebenenschar durchgehen. - Lagebeziehung feststellen:
Man sieht recht schnell, dass die Ebenen wohl nicht parallel zueinander sind. Aber man muss schon sehr viel Glück haben, um zu sehen, dass es ein Ebenenbüschel ist. Um einben entsprechenden Verdacht zu bestätigen, konstruiert man einfach eine zweite Ebenenschar E_b: 2b x + 2y + (2 – b) z = 5b + 2, die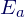 gleicht (Schieberegler nicht vergessen!). Wenn man nun bei
gleicht (Schieberegler nicht vergessen!). Wenn man nun bei 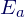 und
und 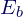 den Parametern andere Werte gibt, kann man sich über den Befehl Schneide[E_a,E_b] die Schnittgerade konstruieren lassen. Und tatsächlich gibt es eine! 🙂
den Parametern andere Werte gibt, kann man sich über den Befehl Schneide[E_a,E_b] die Schnittgerade konstruieren lassen. Und tatsächlich gibt es eine! 🙂
Wie man möglicherweise sieht, ist die Darstellung im Algebra-Fenster nicht optimal. Für eine Weiterbenutzung der Gerade sollte man ggf. den Richtungsvektor mit einer geeigneten Zahl multiplizieren, damit der Vektor angenehmer wird.
Einen schöneren Stützvektor kann man bekommen, indem man einen Punkt auf der Schnittgeraden platziert (zweite Schaltfläche von links) und diesen auf der Gerade etwas hin und her schiebt, bis man einen schöneren Punkt erhält. Leider erwischt man damit nicht unbedingt exakt die „schönen” Punkte, sondern Punkte, deren Koordinaten viele unbequeme Kommastellen haben. Daher muss man unter Umständen ein wenig selbst rechnen. - Geradengleichung eingeben:
Vorsicht! Vektoren muss man in GeoGebra immer als solche kennzeichnen. Daher muss man folgendes in die Eingabezeile schreiben: Gerade[(1, 0, 2), Vektor[(0, ‑2, 3)]]. Nur dann wir die Gerade korrekt konstruiert. Die Gerade benennen wir in g um. - Schnittpunkt berechnen lassen:
Zunächst stellen wir mit dem Schieberegler a auf 2. Mit dem Befehl Schneide[E_a, g] erhalten wir nun den gesuchten Schnittpunkt.
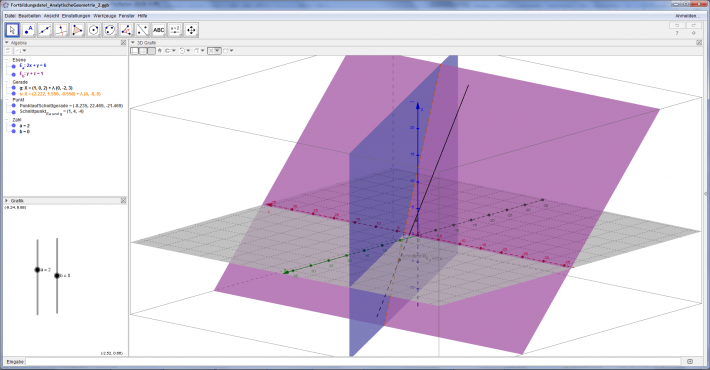
So sollte es am Ende aussehen:
4. Stochastik
Aufgabenstellung
Bestimme die Wahrscheinlichkeit dafür, dass bei 100 Würfen mit einem normalen Würfel mindestens 12 mal und höchstens 20 mal eine 6 gewürfelt wird.
Herangehensweise
- Ansicht einstellen:
Für diese Aufgabe benötigen wir den Wahrscheinlichkeitsrechner, den man im Menü Ansicht auswählen kann. Er öffnet sich in einem eigenen Fenster. - Verteilung einstellen:
Nachvollziehbarerweise benötigen wir hier die Binomialverteilung, also sollten wir das unten links in dem Dropdown-Menü einstellen. - Parameter eingeben:
Wir wählen natürlich n=100 und p=1/6. - Nun ist es wichtig, dass man in dem Bereich unterhalb von n die Variante wählt, bei der man Ober- und Untergrenze eingeben kann.
Nun gibt man die Grenzen ein, nämlich 12 und 20. Sofort gibt GeoGebra das Ergebnis heraus, nämlich 0,7703. Außerdem erhält man eine wunderbare Balkendarstellung, die für die Veranschaulichung sehr nützlich ist.
So sollte es am Ende aussehen:

Eine tolle Anleitung, Stefan – vielen Dank!
Kathrin