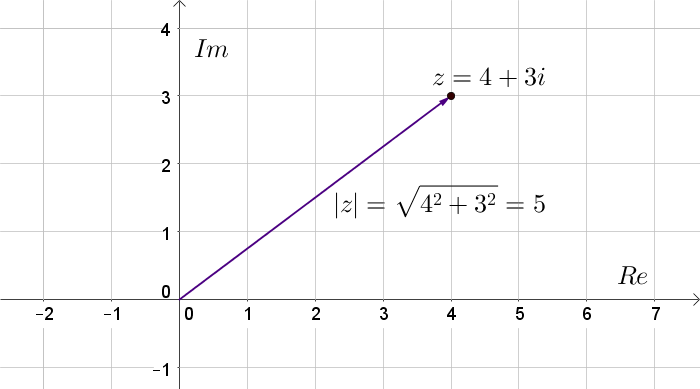
Grundkurs: Kreise und Kugeln (Stand: 2017)
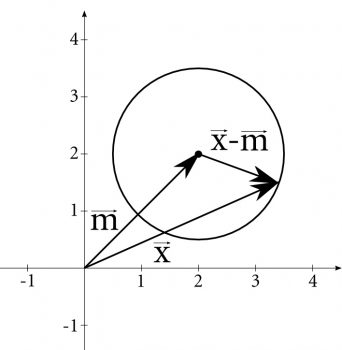 Als Fortsetzung der Vektorrechnung befasst sich dieses Thema mit Kreisen im zweidimensionalen Raum, deren diversen Eigenschaften und mit Lagebeziehungen zu Geraden. Dann geht es in den dreidimensionalen Raum und man betrachtet die Eigenschaften von Kugeln und untersucht die Lagebeziehungen zu Geraden, Ebenen und von Kugeln untereinander.
Als Fortsetzung der Vektorrechnung befasst sich dieses Thema mit Kreisen im zweidimensionalen Raum, deren diversen Eigenschaften und mit Lagebeziehungen zu Geraden. Dann geht es in den dreidimensionalen Raum und man betrachtet die Eigenschaften von Kugeln und untersucht die Lagebeziehungen zu Geraden, Ebenen und von Kugeln untereinander.
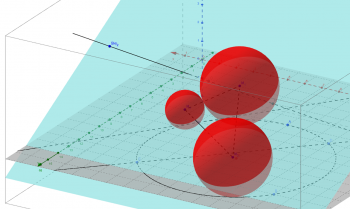 Alle Angaben auf den Blättern sind prinzipiell ohne Gewähr. Die Aufgaben beziehen sich auf das Buch„Cornelsen Mathematik 12.2 LK” (Hessen) aus 2001.
Alle Angaben auf den Blättern sind prinzipiell ohne Gewähr. Die Aufgaben beziehen sich auf das Buch„Cornelsen Mathematik 12.2 LK” (Hessen) aus 2001.
Alle Blätter dürfen nach Belieben heruntergeladen und von Lehrkräften im Unterricht benutzt werden, aber bitte mit Quellenangabe.
GeoGebra-Dateien (Version 5 notwendig):
Kahoot-Quiz
Erstes Quiz zu Abi-Themen (erstellt 2019)
Leistungskurs: Lineare Abbildungen und Determinanten (Stand: 2016)
PDF zu Linearen Abbildungen und Determinanten
»> Link zu einer GeoGebra-Datei von Horst Bennemann zu linearen Abbildungen